Research Areas
Algebra
Our research in Algebra focuses on representations of both finite- and infinite-dimensional Lie algebras, as well as generalized Harish-Chandra modules, approached through algebraic and geometric constructions. We study the structure and representation theory of locally finite Lie algebras and Lie superalgebras, explore generalized flag realizations of homogeneous ind-varieties, and investigate vector bundles of finite rank on these varieties.
Combinatorics
Combinatorics investigates discrete structures and their quantitative and structural properties. Research in this area includes enumerative and analytic combinatorics, graph theory, and combinatorial aspects of topology. Typical objects of study are permutations, partitions, lattice paths, graph embeddings, and maps on surfaces, together with the algebraic and analytic methods used to analyze them. A central focus lies on generating function techniques, bijective constructions, and asymptotic methods that connect exact enumeration with large-scale structural behavior. The research addresses questions about symmetry, structural classification, and limiting phenomena in discrete systems, and explores connections to probability theory, statistical mechanics, and geometric and topological models. Across these directions, combinatorics provides a framework for understanding how local combinatorial constraints shape global structural properties.
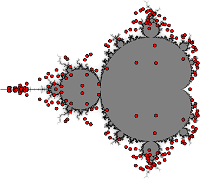
Dynamical Systems
Dynamical systems study the long-term behavior of processes evolving under repeated application of deterministic rules, arising from geometry, algebra, and analysis. Some historically significant examples of dynamical systems come from celestial mechanics (e.g., three body problem), biological systems (e.g., predator-prey models) and the study of atmospheric convection (e.g., Lorenz system). Other prominent examples include classical smooth and measure-preserving systems, the iteration of holomorphic maps in complex dynamics, and actions of Lie groups and lattices on homogeneous spaces. Across these settings, a common focus is on rigidity, statistical properties, and fine geometric structures governing recurrence, stability, and chaotic behavior. The research explores how local analytic or algebraic features influence global dynamical phenomena, and how symmetries and invariants shape the qualitative and quantitative behavior of dynamical systems.
Mathematical Physics / Analysis
Our research in Mathematical Physics focuses on quantum many-body systems, covering topics such as the non-linear Schrödinger equation, derivation of effective dynamics, Bose-Einstein condensates, the Bose-Hubbard model, interaction with radiation fields, Hartree-Fock dynamics, spin wave theory, and the quantum-to-classical transition for thermal equilibrium states. Our methods are based on functional analysis, semiclassical analysis, and the study of partial differential equations.
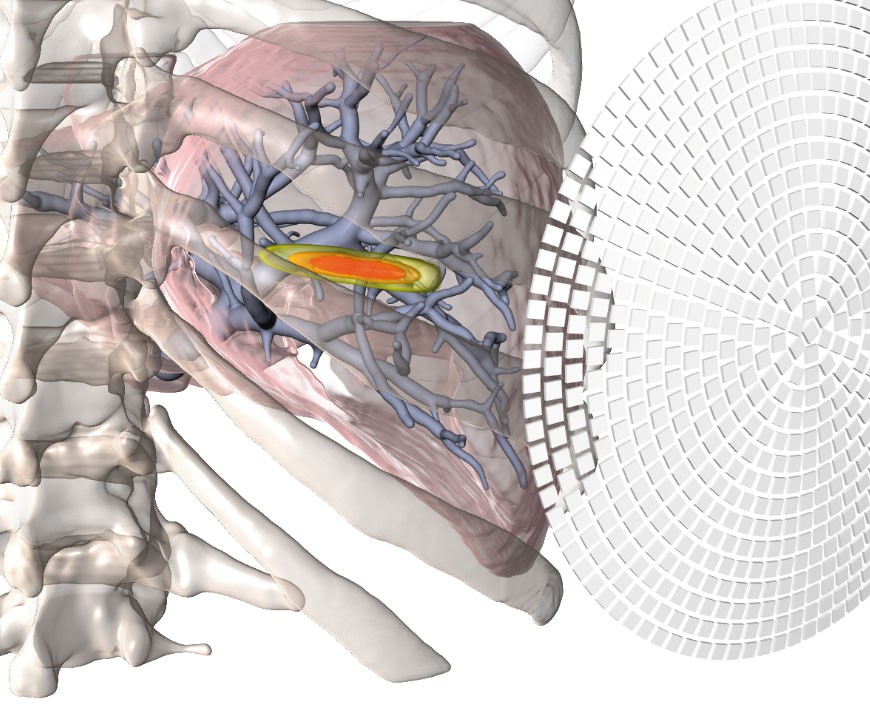
Modeling and Simulation in Medicine
Our research centers on the modelling and simulation of biomedical processes using partial differential equations (PDEs). We develop and analyze mathematical models that contribute to a deeper understanding of physiological phenomena and support applications in medicine. A further focus lies in mathematical image processing, particularly for medical imaging, as well as in scientific visualization based on PDE models. To ensure practical applicability, we emphasize the efficient numerical implementation of these models, including advanced multigrid and multiscale methods for large-scale and high-resolution computations.